Kruskal’s algorithm : Reference

Image	Description
	AD and CE are the shortest arcs, with length 5, and AD has been arbitrarily chosen, so it is highlighted.
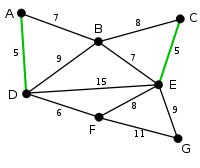	CE is now the shortest arc that does not form a cycle, with length 5, so it is highlighted as the second arc.
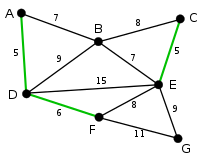	The next arc, DF with length 6, is highlighted using much the same method.
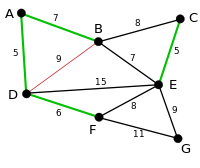	The next-shortest arcs are AB and BE, both with length 7. AB is chosen arbitrarily, and is highlighted. The arc BD has been highlighted in red, because there already exists a path (in green) between B and D, so it would form a cycle (ABD) if it were chosen.
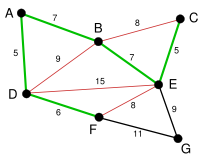	The process continues to highlight the next-smallest arc, BE with length 7. Many more arcs are highlighted in red at this stage: BC because it would form the loop BCE, DE because it would form the loop DEBA, and FE because it would form FEBAD.
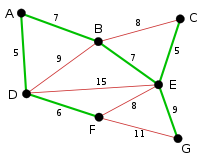	Finally, the process finishes with the arc EG of length 9, and the minimum spanning tree is found.